|
where: G - set of considered models; CR is an external criterion of model g quality from this set; P - number of variables set; S - model complexity; z2 - noise dispersion; T - number of data sample transformation; V - type of reference function. For definite reference function, each set of variables corresponds to definite model structure P = S. Problem transforms to much simpler one-dimensional
when z2= const, T = const, and V = const. Method is based on the sorting-out procedure, i.e. consequent testing of models, chosen from set of models-candidates in accordance with the given criterion. Most of GMDH algorithms, use the polynomial reference functions. General connection between input and output variables can be expressed by Volterra functional series, discrete analogue of which is Kolmogorov-Gabor polynomial: 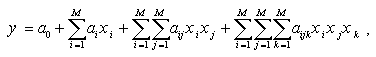
where X(x1,x2,...,xM,); - input variables vector; A(a1,a2,...,aM,); - vector of coefficients or weights; Components of the input vector X can be independent variables, functional forms or finite difference terms. Other non-linear reference functions, such as difference, probabilistic, harmonic, logistic can also be used. The method allows to find simultaneously the structure of model and the dependence of modelled system output on the values of most significant inputs of the system. The GMDH theory solve the problems of: In [12] were obtained the theoretical grounds of GMDH effectiveness as adequate method of robust forecasting models construction, essence of which consists of automatically generation of models in given class by sequential selection of the best of them by criteria, which implicitly by sample dividing take into account the level of indeterminacy.
Since 1968 a big number of GMDH technique implementations
for modeling of economic, ecological, environmental, medical,
physical and military objects were done in several countries.
Self-organizing modeling is based on statistical learning networks, which are networks of mathematical functions that capture complex, non-linear relationships in a compact and rapidly executable form. Such networks subdivide a problem into manageable pieces or nodes and then automatically apply advanced regression techniques to solve each of these simpler problems. Special GMDH peculiarities The main peculiarity of GMDH algorithms is that, when it uses continuous data with noise, it selects as optimal simplified non-physical model. Only for accurate and discrete data the algorithms point out so-called physical model - the most simple optimal, from all unbiased models. It is proved the convergence of multilayered GMDH algorithms [25] and it is proved that shortened non-physical model is better than full physical model on error criterion (for noisy and continuous data for prediction and approximation solving, more simplified Shennon's non-physical models become more accurate [12]). It can be noted, that this conclusion has place in model selection on the basis of models entropy maximization (Akaike approach), in average risk minimizing (Vapnik approach) and in another modern approaches. The only way to get non-physical models is to use sorting-out GMDH algorithms. Usage of sorting-out procedure guarantees selection of the best optimal model from all possible. Regularity of optimal structure of forecasting models change in dependence on general indexes of data indeterminacy (noise level, data sample length, design of experiment, number of informational variables) was shown in [24,25,27]. The special peculiarities of GMDH are following :
The main criteria proposed are: cross-validation PRR(s), regularity AR(s) and balance of variables criterion BL(s). Estimation of their effectiveness (investigation of noise immunity, optimality and adequateness) and their comparison with another criteria was done in detail in [24,25,26,15]. The conditions, under which GMDH algorithm produces the minimum of characteristics are following:
Difference of the GMDH algorithms from another algorithms of structural identification and best regression selection algorithms consists of three main peculiarities: |

